BANGUN RUANG SISI DATAR

 BANGUN RUANG SISI DATAR 

Perlu Anda ketahui, bangun ruang terbagi menjadi beberapa kelompok. Diantaranya adalah bangun ruang sisi datar serta bangun ruang sisi lengkung.

Bangun ruang sisi lengkung sendiri bisa dilihat dari bentuknya yang lengkung, contohnya adalah bola serta tabung. Sementara untuk bangun ruang sisi datar tidak seperti itu? Lalu seperti apa?

Pengertian Bangun Ruang Sisi Datar

Dicermati dari namanya saja, Anda sudah bisa menemukan jawabannya. Terbagi dalam bangun ruang dan sisi datar.

Artinya, bentukan dari bangun ruang yang memiliki sisi-sisi yang datar keseluruhannya. Meskipun sisinya sangatlah banyak, bahkan rumit.

Namun jika ada salah satu sisi atau bentuk ruang yang lengkung, maka bangun ruang tersebut tidak termasuk dalam bangun ruang sisi datar.

Dengan kata lain, bangun tersebut dikatakan bangun ruang sisi datar jika keseluruhan sisinya datar.

Ragam Jenis Bangun Ruang Sisi Datar

Seperti yang dikatakan sebelumnya, bangun ruang ini memiliki sisi datar secara menyeluruh. Artinya, Anda hanya butuh mencermati sebuah bangun ruang saja apakah hanya memiliki sisi datar saja ataukah ada sisi lengkungnya saja.

Jika terdapat percampuran antara sisi datar dan sisi lengkung, jawabannya sudah pasti bukan bangun ruang sisi datar.

Nah, untuk memperjelasnya, ada beberapa jenis bangun ruang tersebut yang diajarkan di bangku sekolahan SMP kelas 8. Diantaranya adalah kubus, balok, limas serta prisma. Seperti apa ciri-ciri dari bangun ruang tersebut?

1. Kubus

Bangun ruang berbentuk persegi biasa dikenal dengan kubus, atau bujur sangkar. Selain itu bangun ruang ini juga dikenal dengan nama bidang enam beraturan yang memiliki tinggi dengan alas yang sama persis. Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat.

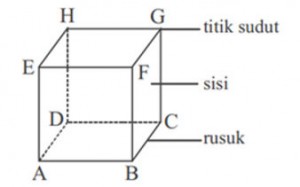
Ada tiga bagian utama dari bangun ruang ini. Diantaranya adalah titik sudut, rusuk serta sisi. Anda bisa memperhatikannya pada bagian gambar kubus di atas.

Untuk penjelasannya, ada sekitar 8 titik sudut yang diwakili oleh titik sudut A, B, C, D, E, F, G, dan H.

Sementara untuk rusuknya berjumlah 12 buah yang sama panjang. Rusuk ini dicontohkan dari AB, BC, CD, EF, FG, GH, EH, AE, BF, CG, DH, serta AD.

Sedangkan untuk sisinya berjumlah 6 buah saja. Yakni sisi ABCD, EFGH, BCGF,ADHE, CDHG, serta ADHE.

Nah, selain tiga bagian utama tadi, ada bagian lain yang disebut dengan diagonal ruang, diagonal bidang serta bidang diagonal. Apa itu?

Diagonal bidang merupakan ruas garis yang sejatinya menghubungkan dua titik sudut yang saling berhadapan. Contohnya adalah AC. Dan untuk jumlahnya sekitar 12 buah.

Sedangkan diagonal ruang merupakan ruas garis yang menghubungkan antara dua titik sudut di dalam sebuah bangun ruang. Jumlahnya ada 4 buah, contohnya adalah AG.

Dan untuk bidang diagonal adalah suatu bidang yang dibatasi oleh dua diagonal bidang serta dua rusuk. Jumlahnya 6 buah saja. Contohnya ABGH, atau ACGE.

Lalu bagaimana dengan rumus menghitung bangun ruang tersebut? Mari perhatikan secara cermat di bawah ini!

• Volume = s x s x s = s³
• Luas Permukaan = 6 s x s = 6 s²
• Panjang Diagonal Bidang = s√2
• Panjang Diagonal Ruang = s√3
• Luas Bidang Diagonal = s²√2

S di sini merupakan penjelasan dari panjang dari sisi kubus atau bangun ruang tersebut.

2. Balok

Banyak sekali benda-benda di sekitarmu yang memiliki bentuk seperti balok. Misalnya, kotak korek api, dus air mineral, dus mie instan, batu bata, dan lain-lain. Sekilas, balok memiliki kemiripan dengan bangun ruang kubus. Kemiripannya tentu saja terdapat pada jumlah rusuk (12 buah), kemudian sisi (6 buah), titik sudut (8 buah), diagonal bidang (12 buah), diagonal ruang (4 buah), serta bidang diagonal (6 buah).

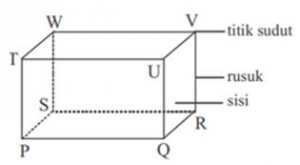
Sementara untuk perbedaannya terletak pada besarnya sisi-sisi bangun ruang tersebut. Artinya, besaran sisi dari bangun ruang berbeda sebagaimana yang dicontohkan dari persegi panjang.

Jika kubus dikenal sebagai bangun ruang yang memiliki sisi-sisi yang sama besar berbentuk persegi, maka balok lebih dikenal sebagai bangun ruang yang memiliki besaran sama dari sisi-sisi yang saling berhadapan, baik dari ukuran sampai bentuknya.

Sedangkan untuk rumus menghitung balok juga berbeda. Anda bisa melihatnya di bawah ini.

• Volume =  panjang x lebar x tinggi = p x l x t
• Panjang Diagonal Bidang = √(p²+l²) atau √(p²+t²) atau √(l²+t²)
• Panjang Diagonal Ruang = √(p²+l²+t²)
• Luas Bidang Diagonal = tergantung dari bidang diagonal yang mana

Untuk keterangannya, p mewakili panjang dari sebuah sisi, kemudian l mewakili lebar, dan t mewakili tinggi dari sebuah bidang.

3. Limas

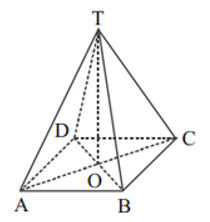
Bangun ruang sisi datar selanjutnya adalah limas. Kamu pasti telah mengenal bangunan piramida di Mesir, bukan? Kamu mungkin juga telah melihatnya, baik itu dari atlas, buku pelajaran, televisi, ataupun melihatnya langsung. Sebagai salah satu keajaiban dunia, piramida digunakan sebagai makam raja-raja Firaun pada jaman dahulu. Definisinya adalah bangun ruang yang memiliki sisi tegak yang berbentuk segitiga yang kemudian berpotongan pada satu titik di puncaknya, serta bentuk alasnya bisa bermacam-macam seperti segitiga, segi empat ataupun segi lima dan lain sebagainya.

Ada beberapa jenis limas. Diantaranya adalah limas segitiga beraturan, limas segi empat beraturan, limas segitiga sembarang serta limas segiempat sembarang.

Jenis-jenis ini dikenali dari bentuk alasnya. Jika alasnya berbentuk segiempat, maka disebut dengan limas segiempat. Dan jumlah sisi tegaknya akan menjadi empat, begitu seterusnya.

Lalu bagaimana dengan tingginya? Tinggi dari limas dilihat dari jarak terpendek dari sisi puncak limas ke bagian alas. Dan tingginya akan selalu tegak lurus dengan titik potong simetri pada bagian alas.

Bagaimana cara menghitungnya? Coba gunakan rumus berikut ini!

• Volume Limas = 1/3 Luas Alas x Tinggi
• Luas Permukaan = Jumlah Luas Alas + Jumlah Luas sisi tegak

4. Prisma

Bangun ruang yang terakhir adalah prisma. Kamu tentu sudah melihat benda-benda yang ditunjukkan pada gambar di atas. Gambar tersebut memperlihatkan .Sepotong kue dan kotak kado. Benda-benda tersebut memiliki bentuk yang sangat unik.Sepintas bangun ruang ini mirip dengan bangun ruang lainnya. Lalu bagaimana cara mengetahui jika bangun ruang tersebut itu prisma atau bukan.

Jawabannya sangatlah sederhana. Anda cukup memperhatikan bidang alas dengan bidang atasnya saja. Kemudian pastikan jika bidang tersebut sejajar dan kongruen.

Dengan kata lain, prisma adalah sebuah bangun ruang yang memiliki bidang alas yang sama persis dengan bagian atas, serta sejajar dan kongruen.

Dari sini, tentu saja akan ada banyak jenisnya. Hal ini disesuaikan dengan bentuk dari alas prisma itu sendiri. Contohnya jika alasnya berbentuk segitiga, maka disebut dengan prisma segitiga. Jika segilima, maka disebut prisma segilima dan seterusnya.

Untuk bagian-bagiannya hampir sama dengan bangun ruang lainnya, hanya saja disesuaikan dengan jenis prisma itu sendiri. Dan untuk tingginya bisa ditemukan dari jarak antara bagian alas dan bagian atas. Sementara untuk cara menghitung volume dan luasnya, Anda bisa menggunakan rumus berikut ini!

• Volume = Luas alas x Tinggi
• Luas permukaan = (2 x Luas Alas) + (Keliling alas x tinggi)

CONTOH SOAL :

 1.    Daerah yang diarsir (merah) pada gambar di bawah ini adalah...

a.    Diagonal ruang
b.    Diagonal bidang (sisi)
c.    Bidang diagonal
d.    Bidang miring
Pembahasan:
Mari kita bahas masing-masing opsi di atas:
a.    Diagonal ruang = garis yang menghubungkan dua titik berhadapan yang tidak sebidang.
b.    Diagonal bidang (sisi) = garis yang menghubungkan dua titik berhadapan pada sisi bangun ruang.
c.    Bidang diagonal = bidang yang menghubungkan dua rusuk berhadapan pada bangun ruang.
d.    Bidang miring = -
Pada gambar di atas, bangun yang diarsir merah merupakan bangun yang dibentuk oleh 2 buah rusuk yang berhadapan.
Jadi, jawaban yang tepat C.

2.    Banyak bidang pada prisma segi-30 adalah...
a.    92
b.    91
c.    33
d.    32
Pembahasan:
Rumus banyak sisi prisma segi – n = n + 2
                                                      = 30 + 2
                                                      = 32 sisi
Jawaban yang tepat D.

3.    Banyaknya rusuk dan sisi prisma segi-8 berturut-turut adalah...
a.    24 dan 10
b.    24 dan 9
c.    16 dan 10
d.    16 dan 9
Pembahasan:
Rumus rusuk prisma segi – n = 3n = 3 (8) = 24
Rumus banyak sisi prisma segi – n = (n + 2) = 8 + 2 = 10
Jawaban yang tepat A.

4.    Alas sebuah limas berbentuk segi-6. Banyaknya rusuk dan sisi limas berturut-turut adalah...
a.    7 dan 12
b.    12 dan 7
c.    7 dan 6
d.    12 dan 6
Pembahasan:
Rumus banyak rusuk pada limas = 2n = 2 (6) = 12
Rumus banyak sisin pada limas = n + 1 = 6 + 1 = 7
Jawaban yang tepat B.

5.    Jika panjang diagonal sisi kubus 6√2 cm, panjang diagonal ruangnya adalah... cm
a.    6√2
b.    6√3
c.    6√5
d.    12
Pembahasan:
Rumus diagonal sisi kubus adalah S√2, dengan S adalah panjang sisi.
Pada kubus di atas panjang diagonal sisinya 6√2 cm, jadi panjang sisi kubusnya 6 cm.
Rumus diagonal ruang pada kubus =S√3
Jadi, panjang diagonal ruang kubus di atas = 6√3 cm
Jawaban yang tepat B.

 Soal No. 6
Sebuah bak mandi berbentuk kubus dengan ukuran panjang sisi 80 cm. Jika bak mandi diisi dengan air kran yang memiliki debit 1 500 cm³ / detik, tentukan waktu yang diperlukan untuk mengisi bak mandi dari kondisi kosong hingga penuh!

Pembahasan
Volume bak mandi adalah
= 80 x 80 x 80
= 512000 cm³

Waktu yang diperlukan
= volume : debit air
= 512000 : 500 = 1024 detik
= 17,01 menit


Soal No. 7
Sebuah kubus dengan rusuk S diperkecil sedemikian rupa sehingga menjadi kubus 1/3 S. Panjang diagonal kubus kecil itu 6√3 cm. Panjang kubus semula adalah...
A. 6 cm
B. 12 cm
C. 18 cm
D. 24 cm
(Ebtanas 1989)

Pembahasan
Berikut untuk mencari hubungan panjang sisi kubus dengan diagonal ruangnya



Dari data soal d = 6√3 dapat langsung diambil panjang sisi kubus kecil adalah 6 cm. Atau kalau dihitung seperti ini



Untuk kubus besar, panjang sisinya 3 kali yang kecil sehingga panjang sisinya = 3 x 6 = 18 cm

Soal No. 8
Luas seluruh permukaan kubus yang panjang rusuknya 7 adalah...
A. 196 cm²
B. 245 cm²
C. 294 cm²
D. 343 cm²
(Ebtanas 1994)

Pembahasan
Data :
s = 7 cm
Luas permukaaan =....

Luas permukaan = 6 × s × s
= 6 × 7 × 7
= 294 cm²

Soal No. 9
Perbandingan volume dua buah kubus adalah 1 : 27. Tentukan perbandingan luas permukaan kedua kubus!

Pembahasan
Data:
V₁ : V₂ = 1 : 27
Perbandingan luas permukaan adalah = ....

Menentukan perbandingan sisi kedua kubus dari perbandingan volumenya



Perbandingan luas permukaan sebanding dengan perbandingan kuadrat panjang kedua sisi kubus

10.    Panjang seluruh rusuk kubus 192 cm. Luas permukaan kubus adalah...
a.    1.536 cm2
b.    1.152 cm2
c.    256 cm2
d.    96 cm2
Pembahasan:
Panjang seluruh rusuk kubus = 192 cm
12 x sisi = 192 cm (karena jumlah rusuk kubus ada 12)
Sisi = 192 : 12
       = 16 cm
Luas permukaan kubus = 6 x sisi x sisi
                                       = 6 x 16 x 16
                                       = 1.536
Jawaban yang tepat A.

Technologi

Technologi 

Teknologi adalah keseluruhan sarana untuk menyediakan barang-barang yang diperlukan bagi kelangsungan dan kenyamanan hidup manusia.
Penggunaan teknologi oleh manusia diawali dengan pengubahan sumber daya alam menjadi alat-alat sederhana. Penemuan prasejarah tentang kemampuan mengendalikan api telah menaikkan ketersediaan sumber-sumber pangan, sedangkan penciptaan roda telah membantu manusia dalam beperjalanan dan mengendalikan lingkungan mereka. Perkembangan teknologi sekarang ini telah banyak menunjukkan kemajuan yang luar biasa. Banyak hal dari sektor kehidupan yang telah menggunakan keberadaan dari teknologi itu sendiri. Kehadirannya telah memberikan dampak yang cukup besar terhadap kehidupan umat manusia dalam berbagai aspek dan dimensi. Demikian halnya dengan teknologi komunikasi yang merupakan peralatan perangkat keras dalam struktur organisasi yang mengandung nilai sosial yang memungkinkan individu untuk mengumpulkan, memproses dan saling tukar informasi (menurut Rogers,1986). Keadaan yang demikian, dimana sebuah teknologi mampu merubah sesuatu yang belum tentu dapat dilakukan menjadi sebuah kenyataan. Misalnya, kalau dahulu orang tidak dapat berbicara dengan orang lain yang berada di suatu tempat yang berjarak jauh, maka setelah adanya telepon orang dapat berbicara tanpa batas dan jarak waktu.
Dari sinilah, semula dengan ditemukannya berbagai perangkat sederhana, mulai dari telepon, yang berbasis analog, maju dan berkembang terus hingga muncul berbagai perangkat elektronik lainnya. Hingga akhirnya teknologi ini berintegrasi satu dengan lainnya. Teknologi komunikasi yang telah ada merupakan sebuah jawaban dari adanya perkembangan zaman. Hal ini terjadi karena semakin berkembang maju sebuah peradaban manusia maka teknologi pun akan terus mengalami perkembangan untuk menyelaraskan pola peradapan manusia itu sendiri.

Dampak Positif Perkembangan Teknologi Masa Kini

1. Internet Sebagai Media Penghubung
Tak dapat dipungkiri jika Internet adalah hal yang sangat melekat kepada kita. Karena internet memiliki fungsi yang amat banyak. Dengan internet, kita dapat melakukan komunikasi dengan orang yang berada jauh antara kita, kita dapat bertukar file, email, maupun koneksi.
2. Kemudahan Bertransaksi
Salah satu dampak yang bisa kita rasakan adalah kemudahan transaksi dengan pelanggan kita. Kemudahan pembayaran, kemudahan pengiriman, hingga kemudahan mencari order. Karena kita dapat memanfaatkan internet, atau memanfaatkan SMS Banking yang dapat kita manfaatkan sewaktu-waktu.
3. Kemudahan Mencari Informasi
Dengan adanya teknologi masa kini yang semakin berkembang, kita dapat mencari informasi dengan sangat mudah sekali. Kita dapat mencari informasi lowongan pekerjaan, informasi bencana alam, informasi kurs mata uang, hingga informasi lalu lintas.

Dampak Negatif Perkembangan Teknologi Masa Kini

1. Akses Pornografi
Inilah hal yang sangat rentan dalam teknologi masa kini. Karena mudahnya dan bebasnya internet, dapat memudahkan anak untuk mencari konten porno yang dapat berakibat buruk kepada ank kita nantinya. Oleh karena itu, dihimbau kepada keluarga taupun orang tua untuk selalu mengawasi anaknya.
2. Penipuan Online
Hal ini juga sangat rentan terjadi di dalam dunia teknologi masa kini. Dengan adanya teknologi yang terus berkembang, penjahat juga memanfaatkannya untuk kepentingan diri sendiri. Mereka mengembangkan teknologi untuk melakukan kejahatan yang dapat berdampak buruk kepada orang lain. Oleh karena itu, kita diharap waspada dengan hal-hal yang seperti ini.


Berikut ini 8 (delapan) prediksi Dell Technologies seputar teknologi 2018 antara manusia dan mesin dalam keterangan resmi yang diterima Tekno Liputan6.com, Sabtu (6/1/2019) di Jakarta.

1 dari 7 halaman

---

1. AI Akan Ciptakan Lapangan Kerja Baru

Ilustrasi Kecerdasan Buatan. Kredit: Geralts via Pixabay

Dalam beberapa tahun ke depan, AI atau kecerdasan buatan akan mengubah cara kita menghabiskan waktu mengolah data.
Dunia usaha akan memanfaatkan AI untuk melakukan “tugas berpikir” berbasis data, sehingga mereka dapat secara signifikan mengurangi waktu yang dihabiskan untuk mengamati, berdebat, merencanakan skenario dan menguji setiap inovasi baru.
Kawasan Asia Pasifik dan Jepang (APJ) saat ini memimpin inovasi kecerdasan buatan, akan segera melihat sejumlah contoh nyata dari manfaat AI dalam realita bisnis.
Beberapa pakar menyatakan bahwa AI akan mengambil alih pekerjaan manusia, namun AI juga dapat menciptakan lapangan pekerjaan baru dan membuka berbagai peluang baru bagi manusia.
Misalnya, akan ada tipe profesional TI baru yang khusus pada pelatihan dan pengaturan AI. Kawasan APJ akan menjadi pusat dari keahlian-keahlian tersebut, dimana AI akan menjadi keahlian utama tenaga kerja di masa depan.
Tugas berpikir AI akan menonjol di bidang kesehatan, pertanian, dan jasa keuangan. Bagi berbagai organisasi, tantangannya adalah membuktikan nilai bisnis dari teknologi AI dan memastikan mereka memiliki infrastruktur dan sumber daya manusia yang tepat.

2 dari 7 halaman

---

2. Hidup Makin Cerdas

Ilustrasi Internet of Things (IoT). (Doc: Wired)

Mulai 2018, sejumlah langkah besar menanamkan kecerdasan buatan berkecepatan tinggi (near instant) dalam IoT, baik kecerdasan buatan yang diterapkan di perkotaan, bisnis, perumahan, dan kendaraan.
Manusia akan berevolusi menjadi ‘konduktor digital’ dari teknologi dan lingkungan di sekitar. Teknologi akan berfungsi sebagai perpanjangan tangan diri kita. Setiap objek akan menjadi lebih cerdas dan membantu kita menikmati hidup secara lebih cerdas.
Kawasan APJ merupakan pusat inovasi dan implementasi IoT. Jumlah investasi akan terus bertambah dan sejumlah faktor seperti inisiatif pemerintah dan perkembangan 5G akan menjadi pendorong besar.
Jepang, Korea Selatan, Singapura, Australia dan Selandia Baru berada di depan dalam hal kesiapan IoT berkat faktor-faktor tersebut.
Namun demikian, hambatan keberhasilan IoT sama di seluruh dunia, sehingga dibutuhkan kolaborasi untuk mengatasi hambatan-hambatan seperti standarisasi yang tidak konsisten, kondisi teknologi yang tidak seragam, dan kebutuhan mempersiapkan infrastruktur.

3 dari 7 halaman

---

3. Batasan Dunia Nyata dan AR Akan Hilang

Augmented reality (Sumber: CNN Money)

Tidak lama lagi batasan antara dunia ‘nyata’ dan AR akan hilang. AR di tempat kerja akan menyatukan manusia, memungkinkan orang berinteraksi dengan data dengan cara yang belum pernah bisa dilakukan sebelumnya. APJ akan menjadi tempat pengujian aplikasi-aplikasi tersebut, seiring perjalanan kawasan ini menguasai inovasi dan aplikasi AR.
VR akan mengubah industri hiburan dan permainan dalam jangka pendek, berkat fitur pengalaman terintegrasi yang ditawarkan. AR juga diprediksi akan menjadi cara memaksimalkan efisiensi manusia dan memanfaatkan ‘pengetahuan institusional’ tenaga kerja yang terus berkembang.
4. Konsumen Ingin Lebih Digital
Index Digital Transformation Dell Technologies menunjukkan 52 persen perusahaan di wilayah APJ berpendapat bahwa perusahaan mereka akan bangkrut dalam 3-5 tahun dan 83 persen merasa terancam oleh startup digital.
Sekarang saat yang paling tepat untuk mengutamakan pengalaman pelanggan. Dalam satu tahun ke depan, berkat analitik prediktif, Machine Learning (ML) dan AI akan menjadi fitur utama, membantu berbagai perusahaan untuk lebih memahami dan melayani pelanggan mereka saat dibutuhkan atau bahkan sebelum kebutuhan itu muncul.
Konsumen di kawasan APJ mulai menuntut interaksi digital yang cerdas dan berbasis mobile. Mereka juga mengadopsi interaksi berbasis teknologi seperti metode pembayaran alternatif. Tahun 2018, berbagai merek dagang akan dipaksa untuk memenuhi ekspektasi konsumen tersebut.

4 dari 7 halaman

---

5. AI dan VR Kian Dibutuhkan

Pengunjung mencoba teknologi Play Station selama BRI Indocomtech 2017 di Jakarta, Kamis (2/11). Pameran ini memamerkan serangkaian produk gadget, smartphone, virtual reality dan piranti pakai (wearable device). (Liputan6.com/Johan Tallo)

Dalam sepuluh tahun ke depan, teknologi-teknologi baru seperti VR dan AI, akan membantu orang mencari dan bertindak terhadap informasi yang diterima tanpa dipengaruhi emosi atau prasangka eksternal, sembari tetap memberdayakan mereka menerapkan pertimbangan humanis sesuai kebutuhan.
Dalam jangka pendek, AI akan diterapkan dalam proses rekrutmen dan promosi untuk memilah keputusan bias, baik yang dilakukan secara sadar maupun tidak sadar.
Sementara VR akan semakin banyak digunakan sebagai alat wawancara untuk memastikan bahwa pekerjaan diberikan kepada pelamar yang memenuhi syarat, misalnya dengan menyembunyikan identitas pelamar dengan sebuah avatar.
6. e-Sports Kian Populer
Pada 2018, sejumlah besar pemain e-Sports duduk di belakang layar atau menggunakan headset VR untuk berkompetisi dalam dunia rekayasa komputer high-definition.
Dengan ratusan juta pemain dan penonton yang menyaksikan, e-Sports akan menjadi permainan mainstream. Wilayah APJ mulai merealisasikan hal tersebut dengan e-Sports menjadi salah satu ajang olahraga resmi di Asian Games 2022.
China, Hong Kong dan Korea Selatan mulai memperkenalkan e-Sport dengan berbagai pertandingan dan investasi yang dilakukan. Singapura juga sudah mulai membidik para profesional e-Sport lokal dengan mendirikan akademi pelatihan untuk melahirkan juara-juara masa depan.

5 dari 7 halaman

---

7. Perjalanan Menuju Mega-cloud

Foto: www.nostra.ie

Mulai 2018, semakin banyak perusahaan yang beralih ke pendekatan multi-cloud, memanfaatkan kelebihan dari semua model cloud mulai dari publik hingga privat, hosted, managed dan SaaS.
Akan tetapi, seiring meningkatnya perpindahan aplikasi dan beban kerja ke berbagai jenis cloud, pertambahan silo cloud sudah pasti terjadi, yang akan menghambat kemampuan organisasi tersebut untuk sepenuhnya mengeksploitasi inisiatif analitik data dan AI.
Organisasi-organisasi di APJ akan masih menghadapi tantangan untuk mengatur infrastruktur TI mereka agar bisa mengatasi tantangan-tantangan yang ada saat ini namun tetap mempertimbangkan aplikasi-aplikasi di masa depan.
Maka mega cloud akan muncul, di mana pendekatan ini akan menjalin berbagai private dan private cloud untuk dapat bertindak sebagai suatu sistem yang koheren dan holistik dalam satu tampilan gabungan pintar dari seluruh ekosistem TI.

6 dari 7 halaman

---

8. Tahun Penuh Aksi

Koki menyiapkan makanan untuk dibawa oleh pelayan robot di Chennai, India (20/12). Restoran ini merupakan yang pertama di India yang memiliki pelayan robot dengan server otomatis membawa piring dari dapur ke pelanggan. (AFP Photo/Arun Sankar)

Dalam dunia yang kini semakin terhubung, ketergantungan terhadap pihak ketiga semakin besar. Organisasi-organisasi telah menjadi sistem yang sangat terhubung yang keberadaannya merupakan bagian dari sesuatu yang bahkan lebih besar lagi.
Dampak dari kekacauan ini tersebar semakin jauh dan cepat sejak teknologi saling menghubungkan kita dengan cara-cara luar biasa.
Akibat hubungan yang semakin terjalin erat antara manusia dan mesin, kegagalan kecil dapat mengakibatkan kegagalan besar.
Oleh karena itu, tahun ini akan menjadi tahun penuh aksi bagi perusahaan-perusahaan multinasional, terlebih dengan berlakunya berbagai peraturan baru seperti Peraturan Perlindungan Data Umum (General Data Protection Regulation / GDPR) yang akan berdampak pada semua organisasi di kawasan APJ.


Demikianlah perkembangan teknologi yang terjadi pada masa sekarang ini,untuk itu hendaknya kita bisa menjaga diri kita dari hal hal yang buruk agar terhindar dari berbagai persoalan yang rumit. Namun kita juga jangan sampai menutup diri kita dari adanya perkembangan teknologi yang ada pada saat sekarang ini karena itu dapat membuat kita minim pengetahuan oleh karena itu gunakan teknologi dengan bijak dan apa adanya saja.

ART ( SENI ) IN LIFE

ART IN LIFE 

 

ART IN LIFE yang artinya Seni Dalam Hidup adalah postingan blogger saya yang baru. Kali ini saya akan menuliskan sebuah cerita dari seorang guru kepada muridnya mengenai Seni yang ada kaitannya dengan Kehidupan. 

     Melihat katanya saja kalian pasti sudah tahu itu apa, namun semua itu berbeda menurut sebagia orang. Banyak orang mengatakan bahwa seni ( art ) adalah keindahan, kerajinan, karya dll, tetapi kali ini kita akan membicarakan seni yang ada kaitannya dengan kehidupan. Ada salah seorang guru yang bilang kepada saya dan beberapa teman teman saya seperti ini,

" Saya menyukai seni karena seni itu memberikan warna dikehidupan nyata, seni itu seperti wanita kita harus menjaga diri kita sendiri agar tidak terbawa nafsu kecuali kalu memang kita sudah diperbolehkan ( sah ). Begitu juga hidup kita , kita harus menjaganya agar tidak tercebur dalam lumpur yang lengket ( sesuatu yang buruk atau salah )".

      Begitulah yang beliau katakan kepada saya, Dari kata kata itulah saya mulai sadar dan terinspirasi tentunya dengan seni. Seni selalu ada dalam kehidupan kita sehari hari tanpa kita sadari dan tanpa terkecuali. Namun, kita tidak menyadarinya mungkin selama ini sebagian orang berpikir bahwa seni itu ya... itu itu saja, biasa biasa saja. Akan tetapi setelah saya teliti lebih dalam mengenai apa itu seni sebenarnya ternyata seni itu memiliki filosofi yang indah dan luas. Tanpa kita sadari, terkadang kita membuat seni tapi tidak menyadarinya karena kita hanya berpikir bahwa itu pekerjaan yang biasa dan juga hanya berpikir untuk segera menyeesaikan secepatnya. Kita tidak pernah memahami secara keseluruhan, untuk itulah seharusnya kita harus lebih bisa dalam memahami setiap hal yang kita lakukan. 

 " Percuma atau sia sia saja kamu mengerjakan sesuatu jika kamu tidak memahami maksud di dalamnya atau apa yang kamu kerjakan ".

  

        Itulah kata kata yang saya jadikan sebagai prinsip dalam menjalani kehidupan ini. Seperti juga yang dikatakan teman saya kepada diri saya, yaitu

" Jangan pernah memaksa hal yang tidak ingin kamu lakukan karena percuma hasilnya tidaklah ketulusan dari hatimu sendiri melainkan nafsu akan kemauanmu yang tidak ingin kamu lakukan ". 

       Dari kata yang ia ucapkan saya tahu bahwa dalam berseni itu harus disertai dengan ketulusanyang nyata bukan karena paksaan atau apapun. Seni adalah ungkapan dan keindahan atau lebih tepatnya ungkspsn ysng disertai dengan keindahan. Seni itu sendiri memiliki berbagai jenis antara lain, seni patung, seni kriya, seni ukir dll. Sama seperti hidup juga memiliki berbagai warna tergantung kita mau mewarai apa saja pada hidup kita. Seni selalu berubah ubah muai dari dulu hingga sekarang tanpa terkecuali, Hal tersebutlah yang menurut saya juga sama dengan hidup yang selalu berubah ubah menurut zamannya sendiri. Jadi, kesimpulan yang dapa kita ambil adalah bahwa seni selalu ada kaitannya dengan kehidupan, seni adalah ungkapan, seni adalah warna yang beragam. Dimana kamu bisa mengungkapkan segala hal yang tidak dapat kamu ungkapkan secara langsung, dimana kamu bisa memeberikan warna sesuai keinginanmu, diman kamu bisa mengetahui bahwa waktu akan terus berjalan ke depan.

       Tetapi dari semua itu, semuanya masih tetap tuhanlah yang akan memutuskan . Kita hanya boleh untuk menjaga, merawatnya, memperbaikinya serta mengembangkannya saja sementara hasil terakhirnya dan yang akan memutuskan apa yang akan terjadi. Untuk itu saya berharap dari apa yang saya tuliskan kalian bisa belajar mengenai seni sebenarnya bahwa seni itu juga menyenangkan. Seni yang sebenarnya ternyata ada kaitannya dengan hidup yang kita jalani. 

 

   Life is time because that is you must always strong and spirit.....

I KNOW YOU CAN.......

I KNOW YOU CAN.....   

     For that you can doing anything for your life.

     You can doing something do you like or no.

     Because this is art. Art is life and Life is art.